תרגיל
קבעו אם הפונקציה זוגית או אי-זוגית או לא זוגית ולא אי-זוגית:
f(x)=e^{-2x}
תשובה סופית
פתרון מפורט
נבדוק אם הפונקציה:
f(x)=e^{-2x}
זוגית או אי-זוגית או לא זוגית ולא אי-זוגית.
f(-x)=
=e^{-2\cdot (-x)}=
=e^{2x}
קיבלנו
f(-x)=e^{2x}
מכיוון ש-
f(-x)=e^{2x}\neq -e^{-2x}=-f(x)
אז הפונקציה אינה אי-זוגית.
ומכיוון ש-
f(-x)=e^{2x}\neq e^{-2x}=f(x)
וגם
e^{2x}\neq -e^{-2x}=-f(x)
אז הפונקציה גם אינה זוגית.
מכאן, הפונקציה לא זוגית ולא אי-זוגית.
כך נראה גרף הפונקציה:
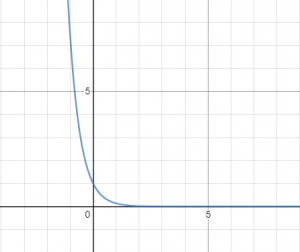
ואפשר לראות מהגרף שהפונקציה לא זוגית ולא אי-זוגית.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

