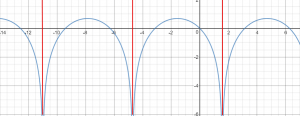
תרגיל
חקרו את הפונקציה:
y=\ln(1-\sin x)
תשובה סופית
פתרון מפורט
פתרון זה זמין רק למנויי האתר שנהנים מפתרונות מוסברים ע"י מתרגלת מצטיינת
מותאם לכל קורסי חדו"א
מנויים ממליצים
"נתקלתי באתר שלך וממש שמחתי כי הוא נורא ברור וענייני" – סיון – ביוטכנולוגיה, מכללת תל חי
"חייבת לציין שהאתר מעולה!" – נעמה – הנדסת מכונות, אונ' בן-גוריון
"המון תודה על העזרה. האתר מדהים!" – דניאל – הנדסת תעשייה וניהול, האונ' הפתוחה
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂