תוכן עניינים:
משוואת קו ישר
משוואת קו ישר אינסופי (משוואה לינארית):
y=ax+b
בנקודה:
(0,b)
הישר חוצה את ציר y.
ובנקודה
(-\frac{b}{a},0)
הישר חוצה את ציר x.
משוואת פרבולה
משוואת פרבולה:
y={(x-a)}^2+b
בנקודה (a,b) יש לפרבולה נקודת קיצון. אם המקדם של x שלילי, אז הנקודה היא נקודת מקסימום, ואם המקדם של x חיובי, אז הנקודה היא נקודת מינימום.
משוואת היפרבולה
\frac{{(x-a)}^2}{c^2}-\frac{{(y-b)}^2}{d^2}
משוואת מעגל
משוואת מעגל בעל רדיוס r ומרכז בנקודה (a,b):
{(x-a)}^2+{(y-b)}^2=r^2
למשוואות מעגל באי-שוויון, משוואות חצאי מעגל וגרפים לחצו כאן.
משוואת אליפסה
משוואת אליפסה:
\frac{{(x-a)}^2}{c^2}+\frac{{(y-b)}^2}{d^2}
מרכז האליפסה – הנקודה (a,b), אורך הרדיוס המקביל לציר x הוא c ואורך הרדיוס המקביל לציר y הוא d.
למשוואות אליפסה באי-שוויון, משוואות חצאי אליפסה וגרפים לחצו כאן.
משוואת מעוין
משוואת מעוין:
|x|+|y|=1
משוואת אסארואידה
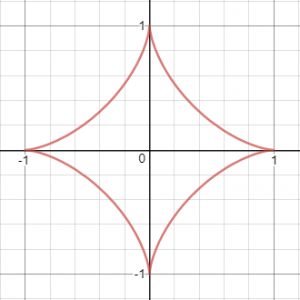
משוואת אסטרואידה:
x^{\frac{2}{3}}+y^{\frac{2}{3}}=1
היא נראית כך:
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה? כתב/י תגובה למטה ואשמח לענות 🙂

