זהויות טרוגונומטריות הן משוואות, הכוללות פונקציות טריגונומטריות, ומתקיימות לכל ערך x בתחום ההגדרה של הפונקציות.
שימוש בזהויות טריגונומטריות עוזר מאוד בפתרון תרגילים, בעיקר כדי לפשט ביטויים מסובכים לחישוב. שליטה בזהויות הטריגונומטריות תקל עליכם מאוד ותחסוך לכם זמן רב בבחינה!
כאן תמצאו את כל הזהויות הטריגונומטריות הנדרשות לפתרון התרגילים.
לחצו כאן לתרגילים ופתרונות המשתמשים בזהויות טריגונומטריות
תוכן עניינים:
- זהויות בסיסיות
- זהויות של סימטריה
- זהויות של זווית כפולה ומשולשת
- זהויות של סכום והפרש זוויות
- זהויות להורדת חזקה
- גרפים
טבלת זהויות טריגונומטריות להורדה
זהויות בסיסיות
\sin^2\theta+\cos^2\theta=1
\tan\theta=\frac{\sin\theta}{\cos\theta}
מזהויות אלו מקבלים את הזהויות:
\cot\theta=\frac{\cos\theta}{\sin\theta}
\cos \theta =\pm\sqrt{1-\sin^2 \theta}
\sin \theta =\pm\sqrt{1-\cos^2 \theta}
\cos \theta =\pm\frac{1}{\sqrt{1+\tan^2 \theta}}
1+\tan^2 \theta=\frac{1}{\cos^2 \theta}
זהויות של סימטריה
\sin(-\theta)=-\sin(\theta)
\cos(-\theta)=\cos(\theta)
\tan(-\theta)=-\tan(\theta)
\sin (\theta+\frac{\pi}{2})=\cos \theta
\sin (\frac{\pi}{2}-\theta)=\cos \theta
\cos(\theta+\frac{\pi}{2})= -\sin \theta
=\cos(\frac{\pi}{2}-\theta)= \sin \theta
זהויות של זווית כפולה ומשולשת
\sin(2\theta)=2\sin\theta\cos\theta
\cos(2\theta)=2\cos^2\theta -1
\cos(2\theta)=1-2\sin^2\theta
\cos(2\theta)=\cos^2\theta-\sin^2\theta
\tan(2\theta)=\frac{2\tan\theta}{1-\tan^2\theta}
\sin(3\theta)=3\sin\theta -4\sin^3\theta
\cos(3\theta)=4\cos^3\theta-3\cos\theta
זהויות של סכום והפרש זוויות
\sin(\theta\pm\phi)=\sin\theta\cos\phi\pm\cos\theta\sin\phi
\cos(\theta\pm\phi)=\cos\theta\cos\phi\mp\sin\theta\sin\phi
\tan(\theta\pm\phi)=\frac{\tan\theta\pm\tan\phi}{1\mp\tan\theta\tan\phi}
הסבר: כאשר יש בנוסחה סימן "פלוס-מינוס", זה אומר שבנוסחה מסתתרות שתי נוסחאות: נוסחה המשתמשת רק בסימן העליון בכל הנוסחה ונוסחה המשתמשת רק בסימן התחתון בכל הנוסחה.
זהויות להורדת חזקה
\sin^2\theta=\frac{1-\cos(2\theta)}{2}
\cos^2\theta=\frac{1+\cos(2\theta)}{2}
\sin^3\theta=\frac{3\sin\theta-\sin (3\theta)}{4}
\cos^3\theta=\frac{3\cos\theta+\cos (3\theta)}{4}
\cos^4 \theta=\frac{3+4\cos (2\theta)+\cos(4\theta)}{8}
\sin^5 \theta=\frac{10\sin \theta-5\sin (3\theta)+\sin (5\theta)}{16}
גרפים
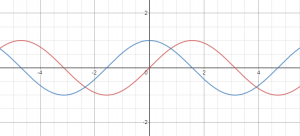
הפונקציה באדום היא
y=\sin(x)
הפונקציה בכחול היא
y=\cos(x)
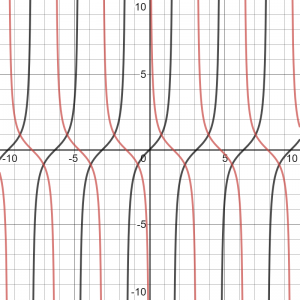
הפונקציה בשחור היא
y=\tan(x)
הפונקציה באדום היא
y=\cot(x)
לחצו כאן לתרגילים ופתרונות המשתמשים בזהויות טריגונומטריות
לחצו כאן להורדה בחינם של קובץ PDF של זהויות טריגונומטריות
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

