גרף הפונקציה
y=\cos(x)
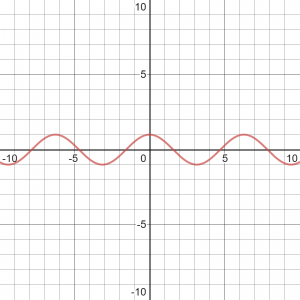
ויחד עם פונקציות נוספות זה נראה כך:
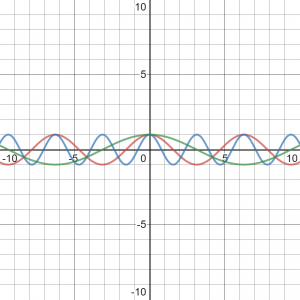
הפונקציה באדום היא
y=\cos(x)
הפונקציה בכחול היא
y=\cos(2x)
הפונקציה בירוק היא
y=\cos(\frac{x}{2})
ערכי הפונקציה cos במעלות צלזיוס
\cos 0\degree=1
\cos 30\degree=\frac{\sqrt{3}}{2}\approx 0.866
\cos 45\degree=\sqrt{\frac{1}{2}}\approx 0.707
\cos 60\degree=\frac{1}{2}=0.5
\cos 90\degree=0
\cos 135\degree=-\sqrt{\frac{1}{2}}\approx -0.707
\cos 150\degree=-\frac{\sqrt{3}}{2}\approx -0.866
\cos 180\degree=-1
ערכי הפונקציה cos ברדיאנים
\cos 0=1
\cos \frac{\pi}{6}=\frac{\sqrt{3}}{2}\approx 0.866
\cos \frac{\pi}{4}=\sqrt{\frac{1}{2}}\approx 0.707
\cos \frac{\pi}{3}=\frac{1}{2}=0.5
\cos \frac{\pi}{2}=1
\cos \frac{3\pi}{4}=-\sqrt{\frac{1}{2}}\approx -0.707
\cos \frac{5\pi}{6}=-\frac{\sqrt{3}}{2}\approx -0.866
\cos \pi=-1
זהויות
\cos (\pi-\theta)=-\cos \theta
\cos (\theta+2\pi)=\cos \theta
\cos (\theta+\pi)=-\cos \theta
\cos (\theta+\frac{\pi}{2})=-\sin\theta
בעזרת הזהויות האלה וערכי הפונקציה לעיל אפשר למצוא ערכים נוספים של הפונקציה.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

