תוכן עניינים:
הגדרת משוואת אליפסה
המשוואה:
\frac{{(x-a)}^2}{c^2}+\frac{{(y-b)}^2}{d^2}=1
היא משוואת אליפסה שהמרכז שלה בנקודה
(a,b)
המרחק שלה מנקודת המרכז לנקודות בהיקף מצד ימין ומצד שמאל הוא c והמרחק שלה מנקודת המרכז לנקודות בהיקף שמעליה ומתחתיה הוא d. מכאן, הפרמטרים c,d חיוביים וגדולים מאפס.
המשמעות: כל הנקודות במישור XY שמקיימות את המשוואה הן נקודות על היקף האליפסה.
כאשר מרכז האליפסה בראשית, כלומר בנקודה (0,0), מקבלים שמשוואת האליפסה היא
\frac{x^2}{c^2}+\frac{y^2}{d^2}=1
משוואת אליפסה שמרכזה בראשית נקראת משוואת אליפסה קנונית.
דוגמה
משוואת האליפסה:
\frac{x^2}{3^2}+\frac{y^2}{2^2}=1
מתארת את האליפסה הקנונית שמרכזה בראשית.
כך נראה גרף האליפסה:
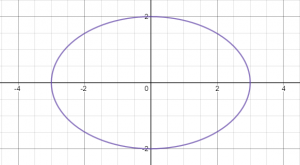
מרכז האליפסה בראשית. האליפסה חותכת את ציר x בנקודות:
x=3,-3
וזה באמת המספר במכנה של השבר עם x.
והאליפסה חותכת את ציר y בנקודות:
y=2,-2
וזה באמת המספר במכנה של השבר עם y.
משוואת אליפסה באי-שוויון
כאשר נתונה משוואת אליפסה באי-שוויון, מקבלים תחום סופי או אינסופי במישור XY.
דוגמה
המשוואה:
\frac{x^2}{2^2}+\frac{y^2}{1^2}\leq 1
\frac{x^2}{4}+\frac{y^2}{1}\leq 1
כוללת משוואה ואי-שוויון:
\frac{x^2}{4}+\frac{y^2}{1}= 1
\frac{x^2}{4}+\frac{y^2}{1}< 1
המשוואה הראשונה מתארת את היקף האליפסה (כמו למעלה), והמשוואה השנייה מתארת את פנים האליפסה. לכן, האי-שוויון
\frac{x^2}{4}+\frac{y^2}{1}\leq 1
מתאר את כל התחום של היקף האליפסה והשטח שבתוך האליפסה. כך זה נראה:
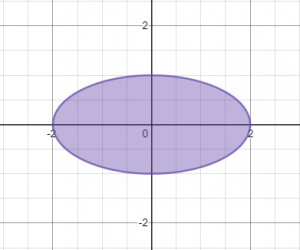
משוואת האי-שוויון:
\frac{x^2}{4}+\frac{y^2}{1}< 1
מתארת רק את פנים האליפסה, ללא ההיקף. כך התחום שלה נראה במישור XY:
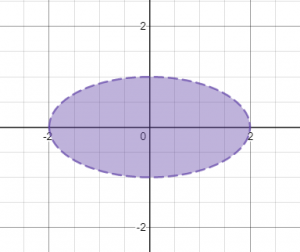
כאן, התחום הוא התחום הסגול ואינו כולל את היקף האליפסה, אלא רק את השטח שבתוך האליפסה.
באופן דומה, מקבלים שהאי-שוויון ההפוך:
\frac{x^2}{4}+\frac{y^2}{1}\geq 1
מתאר את התחום:
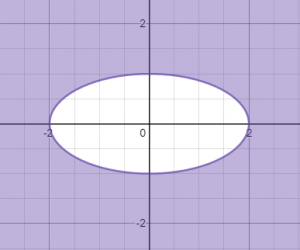
האי-שוויון מתאר את כל התחום הסגול, שהוא היקף האליפסה וגם כל השטח במישור XY שמחוץ לאליפסה. כאן, מתקבל תחום אינסופי.
והאי-שוויון ללא סימן שווה:
\frac{x^2}{4}+\frac{y^2}{1}> 1
מתאר את התחום:
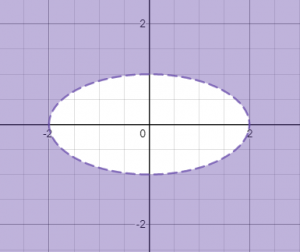
האי-שוויון מתאר את כל התחום הסגול, שהוא כל השטח במישור XY שמחוץ לאליפסה, בלי היקף האליפסה. גם כאן, מתקבל תחום אינסופי.
משוואות של חצי אליפסה
אם נבודד את המשתנה y במשוואת האליפסה הקנונית נקבל:
\frac{x^2}{c^2}+\frac{y^2}{d^2}=1
\frac{y^2}{d^2}=1-\frac{x^2}{c^2}
\frac{y}{d}=\pm\sqrt{1-\frac{x^2}{c^2}}
y=\pm d\sqrt{1-\frac{x^2}{c^2}}
קיבלנו שתי פונקציות:
y_1=d\sqrt{1-\frac{x^2}{c^2}}
y_2=-d\sqrt{1-\frac{x^2}{c^2}}
הפונקציה הראשונה תמיד חיובית, כי שורש תמיד גדול או שווה לאפס, והפונקציה השנייה תמיד שלילית.
דוגמה
עבור d=1, c=2 נקבל את משוואת האליפסה הקנונית:
\frac{x^2}{3^2}+\frac{y^2}{2^2}=1
\frac{x^2}{9}+\frac{y^2}{4}=1
וכשנבודד את המשתנה y נקבל את הפונקציות:
y_1=2\sqrt{1-\frac{x^2}{9}}
y_2=-2\sqrt{1-\frac{x^2}{9}}
הנה הגרפים של הפונקציות:
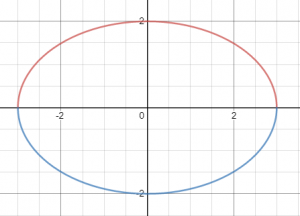
הפונקציה הראשונה באדום – חצי אליפסה חיובית, והפונקציה השנייה בכחול – חצי אליפסה שלילית.
בדומה, אפשר לבודד את המשתנה x ולקבל:
\frac{x^2}{9}+\frac{y^2}{4}=1
\frac{x^2}{9}=1-\frac{y^2}{4}
\frac{x}{3}=\pm\sqrt{1-\frac{y^2}{4}}
קיבלנו שתי עקומות:
x=3\sqrt{1-\frac{y^2}{4}}
x=-3\sqrt{1-\frac{y^2}{4}}
כאן מקבלים שבעקומה הראשונה x תמיד חיובי, ובעקומה השנייה x תמיד שלילי.
וכך העקומות נראות:
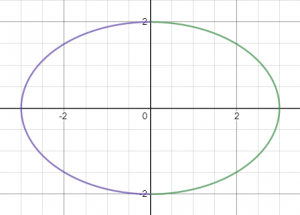
העקומה הראשונה בירוק – בתחום שבו x חיובי, והעקומה השנייה בסגול – בתחום שבו x שלילי.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

