תרגיל
פתרו את האי-שוויון:
x^2+3x+5>0
תשובה סופית
פתרון מפורט
x^2+3x+5>0
זהו אי-שוויון ריבועי. המקדמים שלו הם
a=1, b=3, c=5
המקדם של האיבר הריבועי (a) חיובי, ולכן הפרבולה (גרף המשוואה הריבועית) "מחייכת" (=בצורת קערה). מסימן האי-שוויון צריכים לבדוק עבור אלו x-ים הפרבולה חיובית, כלומר מעל ציר x. נמצא את הפתרונות (=אפסים=שורשים) של המשוואה הריבועית בעזרת נוסחת השורשים. נציב את המקדמים בנוסחה:
x_{1,2}=\frac{-3\pm \sqrt{3^2-4\cdot 1\cdot 5}}{2\cdot 1}=
=\frac{-3\pm \sqrt{-11}}{2}
קיבלנו מספר שלילי בתוך השורש, לכן אין פתרון ממשי למשוואה הריבועית, כלומר המשוואה הריבועית אינה עוברת בציר x. מכיוון שהיא "מחייכת", היא תמיד מעל ציר x. מכאן, האי-שוויון מתקיים לכל x.
ובאמת, הגרף של הפונקציה:
y=x^2+3x+5
נראה כך:
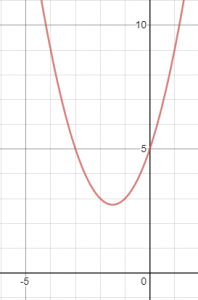
ואפשר לראות שהגרף אכן מעל ציר x לכל x.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

