תרגיל
חשבו את שטח התחום שגבולותיו הם המשוואות:
y-4x=0, x+y=5, y=0
תשובה סופית
פתרון מפורט
נמצא את נקודות החיתוך בין הישרים. לשם כך, נשווה ביניהם ונקבל:
y-4x=0\Longrightarrow y=4x
x+y=5\Longrightarrow y=-x+5
4x=-x+5
5x=5
x=1
נמצא את נקודות החיתוך בין הישרים לציר x. נציב y=0 במשוואה:
y-4x=0
ונקבל:
0-4x=0
4x=0
x=0
נציב y=0 במשוואה:
x+y=5
ונקבל:
x+0=5
x=5
התחום נראה כך:
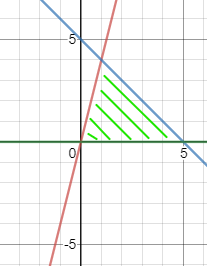
השטח המבוקש מסומן בקווים ירוקים, הישרים בקו אדום ובקו כחול וציר x בקו ירוק.
רואים שהשטח המבוקש הוא סכום של 2 שטחים זרים:
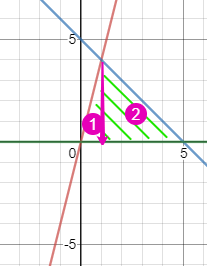
לכן, נחשב כל שטח באינטגרל נפרד ובסוף נחבר את התוצאות.
S=S_1+S_2
נפתור כל אינטגרל בנפרד בעזרת נוסחאות אינטגרציה. נחשב את האינטגרל הראשון:
S_1=\int_0^1 4x dx=
=[4\cdot\frac{x^2}{2}]_0^1=
=[2x^2]_0^1=
זהו אינטגרל מסוים. נציב את גבולות האינטגרציה:
=2\cdot 1^2-2\cdot 0^2=
=2-0=
=2
נחשב את האינטגרל השני:
S_2=\int_1^5 -x+5 dx=
= [-\frac{x^2}{2}+5x]_1^5=
נציב את גבולות האינטגרציה:
=-\frac{5^2}{2}+5\cdot 5-(-\frac{1^2}{2}+5\cdot 1)=
=-\frac{25}{2}+25+\frac{1}{2}-5=
=20-12\frac{1}{2}+\frac{1}{2}=
=8
מכאן, השטח של התחום השני הוא
S_2=8
לבסוף, נסכום את התוצאות:
S=S_1+S_2=
=2+8=10
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

