תרגיל
חשבו את שטח התחום שגבולותיו הם המשוואות:
y=6-x^2, y=x^2-2x-6
תשובה סופית
פתרון מפורט
נמצא את נקודות החיתוך בין שני הפולינומים. לשם כך, נשווה ביניהם ונקבל:
6-x^2=x^2-2x-6
2x^2-2x-12=0
בעזרת נוסחת השורשים נקבל את הפירוק:
(x+2)(x-3)=0
מכאן, נקודות החיתוך הן
x=-2, x=3
התחום נראה כך:
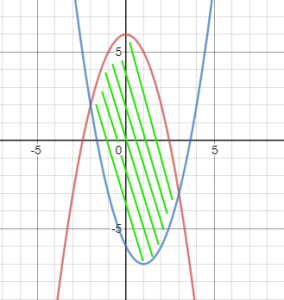
השטח המבוקש מסומן בקווים ירוקים והפולינומים בקו אדום ובקו כחול.
נחשב את השטח בעזרת אינטגרל מסוים:
S=\int_{-2}^3 6-x^2-(x^2-2x-6) dx=
=\int_{-2}^3 -2x^2+2x+12 dx=
נפתור את האינטגרל בעזרת נוסחאות אינטגרציה:
=[-2\cdot\frac{x^3}{3}+2\cdot\frac{x^2}{2}+12x]_{-2}^3=
=[-2\cdot\frac{x^3}{3}+x^2+12x]_{-2}^3=
זהו אינטגרל מסוים. נציב את גבולות האינטגרציה:
=-2\cdot\frac{3^3}{3}+3^2+12\cdot 3-(-2\cdot\frac{{(-2)}^3}{3}+{(-2)}^2+12\cdot (-2))=
=-18+9+36-\frac{16}{3}-4+24=
=27+14\frac{2}{3}=
=41\frac{2}{3}
הערה: אם מחסרים את הפונקציות באינטגרל בסדר הפוך, מקבלים את אותה התוצאה בסימן הפוך, כלומר שלילי. במקרה כזה, נעשה ערך מוחלט על התוצאה ונקבל שטח חיובי כנדרש.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

