תרגיל
מצאו את תחום ההגדרה של הפונקציה:
z(x,y)=\sqrt{1-x^2}+\sqrt{y^2-1}
תשובה סופית
פתרון מפורט
נמצא את תחום ההגדרה. יש בפונקציה שורשים, ולכן נדרוש שהביטויים בתוך השורשים יהיו גדולים או שווים לאפס, כלומר
1-x^2\geq 0
וגם
y^2-1\geq 0
נפתור את האי-שוויון הראשון:
1-x^2\geq 0
זהו אי-שוויון ריבועי. הפרבולה הפוכה ("בוכה"), כי המקדם של האיבר הריבועי שלילי. כמו כן, הפרבולה חוצה את ציר x בנקודות: 1, 1- (אלה השורשים של הפרבולה). לכן, הפתרון של האי-שוויון הוא:
-1\leq x\leq 1
|x|\leq 1
נפתור את האי-שוויון השני:
y^2-1\geq 0
גם זה אי-שוויון ריבועי. הפרבולה הפעם בצורת קערה ("צוחקת"), כי המקדם של האיבר הריבועי חיובי. כמו כן, הפרבולה חוצה את ציר x בנקודות: 1, 1- (אלה השורשים של הפרבולה). לכן, הפתרון של האי-שוויון הוא:
y\leq -1 \text { or } y\geq 1
|y|\geq 1
נחתוך בקשר "וגם" את שני הפתרונות ונקבל:
|x|\leq 1\text{ and } |y|\geq 1
וזו התשובה הסופית.
איך תחום ההגדרה נראה?
הפתרון הוא תחום הכלוא בין ישרים אנכיים ואופקיים.
וכך נראה תחום ההגדרה:
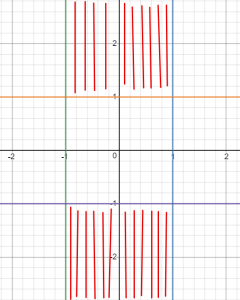
הישרים משורטטים בצבעים: כחול, ירוק, כתום וסגול. תחום ההגדרה מסומן בקווים אדומים. שימו לב שהקווים האדומים ממשיכים עד אינסוף ומינוס אינסוף, ולכן תחום ההגדרה הוא בצורת שני מלבנים אינסופיים.
טיפ: במציאת תחום הגדרה, אפשר לבדוק את התשובה שקיבלתם – פשוט הציבו נקודה מתחום ההגדרה שמצאתם ונקודה שאינה בתחום ההגדרה. הנקודה מתחום ההגדרה צריכה לתת ערך פונקציה מוגדר, ואילו הנקודה מחוץ לתחום ההגדרה צריכה לתת לכם משהו לא מוגדר כמו אפס במכנה, שלילי בתוך שורש, ועוד.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

