תרגיל
מצאו את תחום ההגדרה של הפונקציה:
u(x,y,z)=\sqrt{4-x^2-y^2-z^2}
תשובה סופית
פתרון מפורט
נמצא את תחום ההגדרה. יש בפונקציה שורש, ולכן נדרוש שהביטוי בתוך השורש יהיה גדול או שווה לאפס, כלומר
4-x^2-y^2-z^2\geq 0
נעביר אגפים ונקבל:
x^2+y^2+z^2\leq 4
וזו התשובה הסופית.
תחום ההגדרה נראה כך:
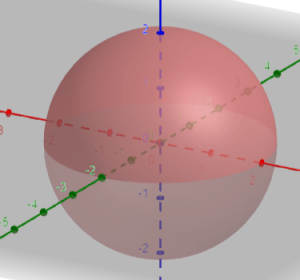
תחום ההגדרה הוא התחום הכולל את כל הנקודות שעל הכדור (שמרכזו בראשית ורדיוסו 2) ואת כל הנקודות שבתוך הכדור.
טיפ: במציאת תחום הגדרה, אפשר לבדוק את התשובה שקיבלתם – פשוט הציבו נקודה מתחום ההגדרה שמצאתם ונקודה שאינה בתחום ההגדרה. הנקודה מתחום ההגדרה צריכה לתת ערך פונקציה מוגדר, ואילו הנקודה מחוץ לתחום ההגדרה צריכה לתת לכם משהו לא מוגדר כמו אפס במכנה, שלילי בתוך שורש, ועוד.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

