תרגיל
חשבו את שטח התחום שגבולותיו הם המשוואות:
y=x^3-3x+1, y=x+1
תשובה סופית
פתרון מפורט
נמצא את נקודות החיתוך בין הפולינום לישר. לשם כך, נשווה ביניהם ונקבל:
x^3-3x+1=x+1
x^3-4x=0
x(x^2-4)=0
נפרק בעזרת נוסחת כפל מקוצר (מעלה שנייה, נוסחה שלישית) ונקבל:
x(x-2)(x+2)=0
מכאן, נקודות החיתוך הן
x=-2, x=0, x=2
התחום נראה כך:
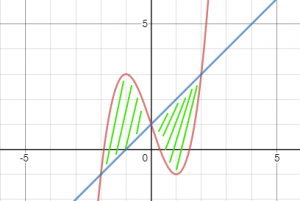
השטח המבוקש מסומן בקווים ירוקים, הפולינום בקו אדום והישר בקו כחול.
רואים שהשטח המבוקש הוא סכום של 2 שטחים זרים. לכן, נחשב כל שטח באינטגרל נפרד ובסוף נחבר את התוצאות.
S=S_1+S_2
נפתור כל אינטגרל בנפרד בעזרת נוסחאות אינטגרציה. נחשב את האינטגרל הראשון:
S_1=\int_{-2}^0 x^3-3x+1-(x+1) dx=
=\int_{-2}^0 x^3-4x dx=
=[\frac{x^4}{4}-4\cdot\frac{x^2}{2}]_{-2}^0=
זהו אינטגרל מסוים. נציב את גבולות האינטגרציה:
=\frac{0^4}{4}-4\cdot\frac{0^2}{2}-(\frac{{(-2)}^4}{4}-4\cdot\frac{{(-2)}^2}{2})=
=0-0-(\frac{16}{4}-4\cdot\frac{4}{2})=
=-\frac{16}{4}+4\cdot\frac{4}{2}=
=-4+4\cdot 2=
=4
הערה: אם מחסרים את הפונקציות באינטגרל בסדר הפוך, מקבלים את אותה התוצאה בסימן הפוך, כלומר שלילי. במקרה כזה, נעשה ערך מוחלט על התוצאה ונקבל שטח חיובי כנדרש.
נחשב את האינטגרל השני:
S_2=\int_0^2 x+1-(x^3-3x+1) dx=
=\int_0^2 x+1-(x^3-3x+1) dx=
=\int_0^2 -x^3+4x dx=
= [-\frac{x^4}{4}+4\cdot\frac{x^2}{2}]_0^2=
נציב את גבולות האינטגרציה:
= -\frac{2^4}{4}+4\cdot\frac{2^2}{2}-(-\frac{0^4}{4}+4\cdot\frac{0^2}{2})=
= -\frac{16}{4}+4\cdot\frac{4}{2}-(-0+0)=
=-4+4\cdot 2=
=4
מכאן, השטח של התחום השני הוא
S_2=4
לבסוף, נסכום את התוצאות:
S=S_1+S_2=
=4+4=8
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

