תרגיל
מצאו את תחום ההגדרה של הפונקציה:
f(x)=\sqrt{1-x^2}
תשובה סופית
פתרון מפורט
נמצא את תחום ההגדרה של הפונקציה. יש בפונקציה שלנו שורש, ולכן צריך לוודא שהביטוי בתוך השורש לא שלילי:
1-x^2\geq 0
קיבלנו אי-שוויון ריבועי. לכן, נפתור את המשוואה הריבועית:
1-x^2=0
הפתרונות (= אפסים = שורשים) של המשוואה הם:
x_1=1, x_2=-1
כמו כן, המקדם של האיבר הריבועי שלילי (1-), ולכן הגרף נראה כפרבולה הפוכה (= קערה הפוכה = "בוכה"). זה נראה כך:
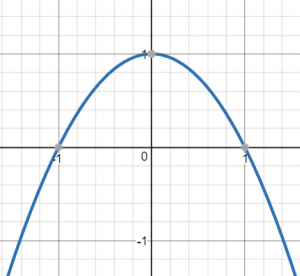
נחזור לאי-שוויון:
1-x^2\geq 0
צריך לבדוק מתי המשוואה שפתרנו לא שלילית, כלומר מתי הגרף לא מתחת ציר x. ורואים מהשרטוט לעיל שזה קורה כאשר מתקיים
-1\leq x\leq 1
זו התשובה הסופית.
עזרתי לך להבין את החומר? מצאת טעות? יש לך שאלה בנוגע לפתרון זה? כתב/י תגובה למטה ואשמח לענות 🙂

